Illegittimità nei rapporti di mutuo e di Leasing
In ossequio alla Legge 108/96 in materia di usura ed alle istruzioni della Banca d'Italia, i criteri utilizzati ai fini del calcolo, oltre alla struttura del rimborso finanziario, sono tutte le spese accessorie obbligatorie inerenti l’erogazione, la fruizione e l’estinzione del finanziamento, come ad esempio: spese di istruttoria pratica, commissioni d'incasso, assicurazioni obbligatorie, interessi di preammortamento, nonché, penali di anticipata estinzione, ecc., non rientrano a far parte dei parametri che incidono sul T.A.E.G. i bolli statali, le tasse e le assicurazioni non obbligatorie.
E' necessario evidenziare che proprio recentemente la Cassazione Civile con sentenza nr. 350 del 2013 ha sancito che gli interessi moratoti vanno sommati a quelli convenzionali ai fini dell'accertmento del superamento o meno della soglia usuraria ab origine ovvero in sede di sottoscrizione di contratto.
E’ utile poi evidenziare che il T.A.E.G. (o ISC) deriva dalla Direttiva 87/102/Cee e si utilizza, come visto, per determinare il costo effettivo dei finanziamenti con restituzione rateale o comunque finanziamenti a “tempo determinato”, ossia tutti quei finanziamenti per i quali è conosciuto in anticipo il periodo di durata del prestito. In altre e più semplici parole, si può affermare che, conoscendo il capitale prestato, la durata del prestito, e tutti i costi e gli oneri (interessi e spese) applicati, è possibile determinare il tasso effettivo globale applicato annualmente (T.A.E.G.), pertanto, il T.A.E.G. è determinabile a priori in quanto ognuna delle variabili della formula di cui infra è conosciuta prima della erogazione del finanziamento. La Direttiva Cee richiamata ha opportunamente introdotto l’entità numerica T.A.E.G. al fine di impedire che, come accadeva in maniera evidente per i prestiti (siano essi mutui, finanziamenti, anticipazioni, aperture di credito in conto corrente, ecc), il soggetto erogante il prestito mascherasse il costo effettivo del denaro nascondendolo dietro variegate voci di costo diversamente nominate e, che, comunque, costituivano una remunerazione aggiuntiva o interesse aggiuntivo (rispetto al T.A.N.) pagato dal fruitore del denaro. In definitiva, il T.A.E.G. indica il costo effettivo del finanziamento espresso in percentuale.
Riportandomi integralmente a quanto dinanzi esposto riguardo al T.A.E.G., si può procedere al calcolo dell'ISC (equivalente del TAEG).
Preciso che, in stretta aderenza al disposto di cui all’art. 2 della Legge 108/96 ai fini della calcolo del T.A.E.G. si tiene conto di tutte le spese correlate all’erogazione del credito tranne le imposte e le tasse.
Si può procedere al calcolo del T.A.E.G. utilizzando il metodo dell’iterazione, in altre parole, si tratta di ottenere la misura di i (ossia del tasso effettivo applicato al finanziamento) con una interpolazione della stessa formula mediante la quale la Banca ha conteggiato gli interessi del finanziamento in esame, peraltro, detto metodo, rappresenta l’unica metodologia di calcolo pienamente legittima e riconosciuta anche dalla Banca d’Italia nelle Istruzioni dettate per la rilevazione del T.A.E.G. con apposita Circolare e dove vengono riportate le fonti normative a cui si deve far risalire tutta la problematica legata alla corretta determinazione dell’effettivo costo del danaro, ossia: Direttiva 87/102/Cee, Legge 154/92, e la Legge 108/96.
Il primo passaggio affinché si possa implementare la formula è attualizzare tutte le spese correlate alla erogazione, fruizione ed estinzione del finanziamento e dettagliatamente esposte prima, alla data di erogazione dei singoli finanziamenti al saggio d’interesse applicato dalla Banca.
Successivamente, al fine dell’esatta attualizzazione delle spese, si è reso necessario calcolare con precisione i giorni trascorsi dalla data di erogazione dei finanziamenti (coincidente con la data in cui attualizzare le somme) e la data in cui si è verificata la singola spesa onde ottenere il valore attualizzato di ogni singola spesa (come si è in precedenza esposto da qui l’importanza della cristallizzazione delle date afferenti le spese) al tasso d’interesse identico a quello in base al quale è stato concesso il finanziamento.
L’importo di Ao va successivamente sottratto all’importo netto del finanziamento erogato; solo in quest’ultima fase, quindi, una volta calcolati tutti gli elementi indispensabili si può applicare la formula del calcolo del T.A.E.G. attraverso il metodo dell’iterazione:

           

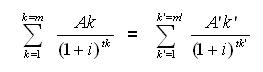
Dove:
i: è il T.A.E.G. annuo, che può essere calcolato quando gli altri termini dell’equazione sono noti nel contratto;
K: è il numero d’ordine di un “prestito”;
K’: è il numero d’ordine di una “rata di rimborso”;
Ak: è il numero d’ordine del “prestito” numero K;
A’k,: è l’importo della “rata di rimborso” numero K;
m: è il numero d’ordine dell’ultimo “prestito”;
m’: è il numero d’ordine dell’ultima “rata di rimborso”;
tk: è l’intervallo espresso in anni e frazioni di anno tra la data del “prestito” n.l e le date degli ulteriori “prestiti” da 2 a m;
tk,: è l’intervallo espresso in anni e frazioni di anni tra la data del “prestito” n.l e le date del “rate di rimborso” da 1 a m’;
dove, per “rata di rimborso” si intende ogni pagamento a carico del cliente relativo al rimborso del capitale, degli interessi e degli oneri, per “prestito” si intende ciascuna erogazione eseguita dal creditore per effetto di uno stesso contratto.
In pratica il valore attuale dei flussi di cassa corrispondenti ai vari importi corrisposti dalla Banca al cliente a titolo di prestito nelle diverse epoche deve essere uguale al valore attuale degli importi corrisposti dal cliente al soggetto finanziatore a titolo di rimborso (principio dell’equivalenza dei tassi noto in matematica finanziaria).
Il T.A.E.G. O ISC è il tasso di interesse che realizza tale uguaglianza.

Violazione Principio dell'equivalenza dei tassi.
Ulteriore profilo di illegittimità che frequentemente si rileva nei contratti di mutuo e di leasing è l'indicazione da parte della banca in contratto di un tasso effettivo inferiore rispetto a quello realmente applicato, portando come conseguenza che il correlato piano di ammortamento nel quale viene esplicitato il calcolo della rata, è errato per eccesso.
Infatti, si verifica che la modalità di applicazione del tasso nominale indicato non è corretta.
In sostanza, le banche non operano correttamente l’applicazione i tassi di interesse, sia per la fase di preammortamento, che per quella di ammortamento. Per spiegarlo, operiamo un esempio: per poter determinare il tasso su base mensile, ha semplicemente diviso il tasso annuale per 12. In altri termini, per la banca, un tasso annuale del 6,20% corrisponde ad un tasso mensile del 0,5167%
Tutto ciò non è corretto, da un punto di vista di matematica finanziaria.
Si veda a tal proposito “Esercizi di matematica finanziaria: regimi finanziari, rendite e ammortamenti”, Università Ca' Foscari di Venezia – Dipartimento di matematica applicata, riportato ampiamente per stralcio infra:

 

 

 

 

Ed infatti, la formula di matematica finanziaria da applicare per ottenere da un tasso annuale quello semestrale non è 
Saggio di interesse semestrale = (saggio annuale /2)
ma
Saggio di interesse semestrale = (1 + saggio annuale) 1/2 -1
poiché
ik = (1+i)1/k-1
Allo stesso modo, per ottenere da un tasso da un tasso annuale quello mensile non è corretto operare nel seguente modo
Saggio di interesse mensile = (saggio annuale /12)
ma
Saggio di interesse mensile = (1 + saggio annuale) 1/12 -1
Alcune banche ed istituti applicano tale corretta formula, e quindi non maggiorano la rata di indebiti importi a titolo di interessi.
Si veda ad esempio il seguente piano di ammortamento:
In detto contratto era stato pattuito un tasso di interesse nominale del 4,15% con rata semestrale.
Ebbene, l’Istituto erogante non ha calcolato il tasso semestrale dividendo semplicemente per due quello annuale (quindi il tasso applicato non è il 2,075%, ma il 2,053907323%, corrispondente a (1 +4,15%) 1/2 -1.
Sia la teoria che la migliore pratica confermano quindi la tesi riportata nella presente relazione.
In genere, però, vediamo come la banca opera per il calcolo della rata, e successivamente il calcolo corretto.
Calcolo della rata errato (per eccesso in suo favore) operato dalla banca:
importo del finanziamento euro 190.000,00.
rimborso 240 rate mensili posticipate
tasso annuale 6,20%
La banca ha quindi operato in questo modo:
tasso mensile = tasso annuale/12, quindi 6,20%/12, quindi 0,516667%.
Quindi, secondo la formula di matematica finanziaria dell’ammortamento francese la rata è uguale a
R= ______ 190.000,00_________ = € 1.383,21
1-(1+0,516667%.)-240
0,516667%

Ed infatti il piano di ammortamento indica una rata di complessivi € 1.388,61, pari ai predetti € 1.383,21 maggiorati di € 5,38 a titolo di assicurazione.
Calcolo della rata corretto:
Occorre calcolare in primo luogo il tasso mensile equivalente a quello annuale:
tasso mensile = (1 + saggio annuale) 1/12 -1
quindi tasso mensile = 0,5025412% e non 0,516667% come utilizzato dalla banca nell’ammortamento de quo.
Quindi, secondo la formula di matematica finanziaria dell’ammortamento francese la rata è uguale a
R= ________ 190.000,00_________ = € 1.364,56
1-(1+0, 5025412%.)-240
0, 5025412%

Di conseguenza, si verifica che la banca nel contratto indica un tasso di interesse, mentre nel concreto ne ha utilizzato uno più alto (ovvero, ha applicato in modo scorretto la formula di matematica finanziaria, addebitando rate superiori rispetto al dovuto).
Applicando la corretta formula di matematica finanziaria al piano di ammortamento, ho ottenuto i risultati riportati sub all.3.
Trova allora applicazione a mio giudizio il principio dettato dalla ben nota sentenza emessa dal Tribunale di Bari, Sezione distaccata di Rutigliano, in data 29 ottobre 2008 e la Sentenza del Tribunale di Larino nr. 119 del 2012: “Ad avviso del Giudicante, il tasso nominale di interesse pattuito letteralmente nel contratto di mutuo non si può assolutamente maggiorare nel piano di ammortamento, né si può mascherare tale artificioso incremento nel piano di ammortamento, poichè il calcolo dell’interesse nel piano di ammortamento deve essere trasparente ed eseguito secondo regole matematiche dell’interesse semplice (..) I contratti di mutuo per cui è causa sono mutui con rimborso frazionato, in cui alla banca, durante il rapporto, si restituisce ratealmente il capitale, originariamente prestato, prima della scadenza finale del mutuo stesso: i mutui de quibus vengono estinti con una serie di pagamenti (rate), effettuati dal debitore. La rata del mutuo con rimborso frazionato si è calcolata, però, nel caso in esame, con la formula del c.d. interesse composto, non prevista nella parte letterale del medesimo contratto, che comporta la crescita progressiva del costo, comprendendo di fatto degli interessi anatocistici. La CTU ha evidenziato un aumento del costo effettivo del rapporto, conseguente alla divaricazione fra il tasso nominale e quello effettivo: cresce quest’ultimo con il crescere del frazionamento del pagamento, poiché più sono le rate, più costa il mutuo".
Il Tribunale di Bari - Sezione Distaccata di Rutigliano nonchè il Tribunale di Larino – Sezione distaccata di Termoli n.119/2012- hanno dichiarato l’annullamento parziale dei contratti di mutuo sopra indicati ed in particolar modo, ai sensi dell’art. 1284 c.c., 1283 c.c. e 1419 c.c., la nullità della clausola dell’interesse ultralegale nella parte in cui vi è stata accertata la difformità tra tasso contrattuale dichiarato nella parte letterale ed il superiore tasso numerico effettivamente applicato nel piano di ammortamento allegato al medesimo contratto, (…)”.
A mio giudizio è indubbio che, poiché il tasso effettivo indicato in contratto è inferiore rispetto a quello realmente applicato, e poiché anche il tasso nominale è stato applicato in modo scorretto, ciò ha determinato i seguenti effetti giuridici:
1. violazione art.1284 c.c., poiché in modo surrettizio, per messo del piano di ammortamento, la banca ha incrementato la remunerazione del capitale oltre la misura contrattualmente prevista e concordata dalle parti;
2. violazione art.1346 c.c., perchè le determinazione della misura dei frutti a remunerazione di un mutuo può avvenire o attraverso una diretta indicazione numerica o convenendo il piano di ammortamento. Nel contratto oggetto di esame la pattuizione del tasso di interesse ultralegale contiene entrambe le indicazioni, ma esse sono contraddittorie e confliggenti tra di loro: nel contratto si indica un TAN, nel piano di ammortamento se ne applica un altro. L'oggetto del contratto non è quindi determinato né determinabile;
3. violazione art. 1347 c.c., poiché emerge in modo evidente come la banca nelle trattative e nella formazione del contratto non si sia comportata secondo buona fede;
4. violazione art. 1375 c.c., poiché la banca, addebitando interessi in misura superiore a quanto esplicitamente pattuito nel contratto, non lo ha eseguito secondo buona fede.
La conseguenza è la nullità della pattuizione (o meglio delle pattuizioni) del tasso ultralegale, e la sua sostituzione con il tasso legale.
Emerge, quindi, in favore del mutuatario un credito nei confronti della banca applicando il tasso di interesse legale (senza anatocismo) dato dalla differenza tra le rate pagate e quelle ricalcolate al tasso legale.